A. Membentuk Kurva IS dengan pendekatan 2 Diagram
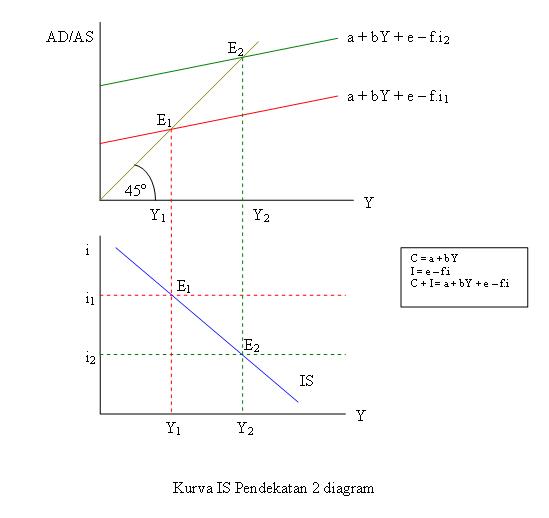
2. Titik E1 pada diagram pertama terbentuk dari perpotongan antara kurva a + bY + e – f.i1 dan garis 45o.
3. Titik E1 pada diagram kedua merupakan perpotongan garis yang ditarik dari titik E1 pada diagram pertama dengan garis i1 pada diagram kedua.
4. Bila tingkat bunga pada i2, maka kurva permintaan agregat adalah pada kurva a + bY + e – f.i2, pendapatan nasional equilibrium pada Y2.
5. Titik E2 pada diagram pertama terbentuk dari perpotongan antara kurva a + bY + e – f.i2 dan garis 45o.
6. Titik E2 pada diagram kedua merupakan perpotongan garis yang ditarik dari titik E2 pada diagram pertama dengan garis i2 pada diagram kedua.
7. Dengan menghubungkan titik E1 dan E2 pada diagram kedua, didapatkan kurva IS.
Dari uraian ini kurva IS bukan kurva yang menerangkan hubungan fungsional antara tingkat bunga dengan pendapatan, akan tetapi merupakan tempat kedudukan setiap tingkat bunga yang menghasilkan pendapatan ekuilibrium di mana penawaran agregat sama dengan permintaan agregat. Kurva IS dapat juga ditafsirkan sebagai multiplier, yaitu perubahan pada pendapatan sebagai akibat pengurangan tingkat bunga, Kurva IS dapat juga ditafsirkan sebagai elastisitas bunga yaitu % perubahan pada pendapatan nasional sebagai akibat perubahan % tingkat bunga.
B. Membentuk Kurva IS dengan pendekatan 4 Diagram
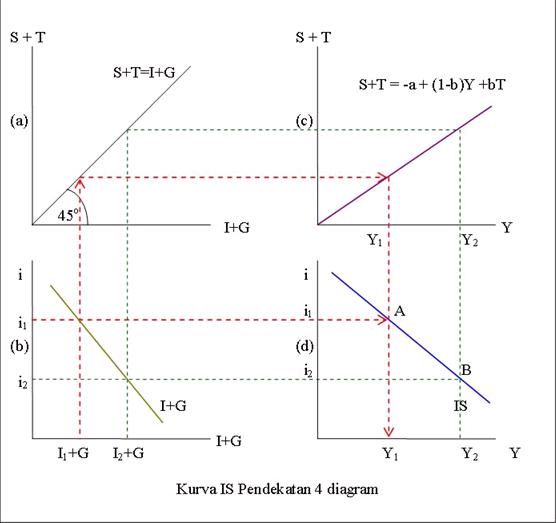
1. Kuadran (a) adalah kuadran yang menggambarkan keseimbangan antara S dengan I dan antara T dengan G. Dalam perekonomian diasumsikan bahwa semua saving diinvestasikan sehingga S = I, yaitu income dalam ekuilibrium. Demikian juga penerimaan pajak (T) dikeluarkan oleh pemerintah (G), sehingga akhirnya I+G = S+T.
2. Kuadran (b) adalah kuadran investasi (I) dan pengeluaran pemerintah. Diasumsikan bahwa investasi dipengaruhi tingkat bunga (I = e – f.i), sedangkan pengeluaran merupakan variabel otonomus (G = Go).
3. Kuadran (c) merupakan diagram penabungan tambah pajak (sebagai padanan dari kuadran (b)). Persamaan penabungan S = -a + bY – bT.
1. Pada tingkat bunga i1 didapatkan titik A pada kuadran (d).
2. Pada tingkat bunga i2 didapatkan titik B pada kuadran (d),
3. Melalui titik A dan titik B dapat dihubungkan kurva IS pada kuadran (d).
Definisi kurva IS pada pendekatan empat kuadran sama dengan dengan kurva IS pada pendekatan dua kuadran. Kurva IS adalah kedudukan kombinasi tingkat bunga dengan pendapatan di mana terjadi keseimbangan antara aggregate demand dan supply, yaitu S + T = I + G.
Pada pendekatan empat kuadran memiliki kelebihan pada kuadran (c). Pada kuadran (c) menjelaskan perubahan variabel penabungan dan perpajakan dapat dianalisis pengaruhnya terhadap kurva IS. Kurva IS dengan pendekatan 2 diagram lebih ringkas dibandingkan dengan pendekatan 4 diagram.
C. Membentuk Kurva LM dengan pendekatan 2 Diagram
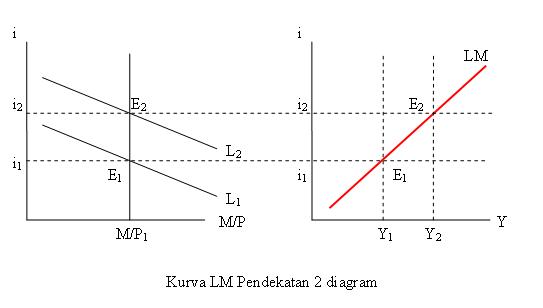
2. Pada penghasilan tertentu ada permintaan uang, kurva permintaan uangnya adalah L1 = kY – h.i.
3. Perpotongan kurva permintaan uang (M/P1) dan penawaran uang (L1) terletak pada titik E1 dan menentukan tingkat bunga i1.
4. Apabila pendapatan bertambah maka kurva permintaan terhadap uang menjadi L2 dan memotong kurva penawaran uang pada E2 sehingga menentukan tingkat bunga i2.
5. Titik Y1 penghasilan yang bersifat “Given” kedua tingkat bunga i yang terbentuk pada diagram sebelah kiri (permintaan dan penawaran_, kemudian karena penghasilan naik yaitu menjadi Y2, maka permintaan terhadap uang menjadi L2 yang menghasilkan tingkat bunga i2 maka terbentuk kurva LM.
Kurva LM menggambarkan tempat kedudukan kombinasi tingkat bunga dengan pendapatan, di mana menghasilkan persamaan antara permintaan dan penawaran uang (ekuilibrium). Kurva LM juga menggambarkan pasar uang dalam keadaan ekuilibrium, pada titik-titik sepanjang kurva LM pasar uang ada dalam keadaan ekuilibrium. Metode dua kuadran lebih langsung (straight forward) membentuk kurva LM daripada metode empat kuadran.
D. Membentuk Kurva LM dengan pendekatan 4 Diagram

1. Pada tingkat pendapatan Y1, ada permintaan uang untuk transaksi sebesar M1t.
2. Dari perpotongan kurva penawaran uang dan permintaan uang untuk transaksi sebesar M1t dapat ditentukan permintaan uang untuk spekulasi sebesar M1SP (Mo = M1t + M1SP).
3. Karena ada permintaan uang untuk spekulasi sebesar M1SP, dapat ditentukan tingkat bunga sebesar i¬1 (Kurva MDSP merupakan fungsi dari tingkat bunga) sehingga diperoleh titik A.
4. Apabila tingkat pendapatan naik menjadi Y¬2, permintaan uang untuk transaksi juga naik menjadi M2t, sehingga permintaan uang untuk spekulasi turun menjadi M2SP (diasumsikan penawaran uang tetap Mo).
5. Tingkat bunga i2 ditentukan dari perpotongan permintaan uang untuk spekulasi dan kurva permintaan uang untuk spekulasi MDSP.
6. Perpotongan tingkat bunga i2 dan pendapatan Y2 menentukan titik B.
7. Kurva LM terbentuk dengan menghubungkan titik A dan B.
Leave a Reply