Fungsi Produksi (Contoh Soal)
Bila diketahui bahwa fungsi produksi barang X dapat dirumuskan dalam format Cobb-Douglas Function Q = 5.K1/4L3/4 di mana Q0 = 1.000 unit
Diminta:
-
Hitunglah least-cost combination penggunaan input K dan L bila r = Rp. 10.000 per machine hour, dan w = Rp 5.000 per man hour.
-
Hitung kembali jawaban soal (a) bila Q’ = 1.100 dan Q” = 1.500
-
Buatlah rekapitulasi yang menggambarkan Cost Function
-
Susun kembali rekapitulasi tersebut pada soal c bila cost of capital naik 10% dan labor cost naik 5%
-
Dapatkah saudara menggambarkannya dalam bentuk grafik
Jawaban :
-
C = r.K + w.L
Meminimumkan biaya dengan kendala fungsi produksi
Dengan SOP optimasi:
minimumkan : C = r.K + w.L
yang memenuhi :
kendala : Q = 5.K1/4L3/4
fungsi sasaran : G = r.K + w.L – λ(5.K1/4L3/4 – Q)
Syarat primer:
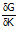= 0 ; 
= 0
Sehingga:
= r – λ.5.(1/4).K-3/4L3/4 = 0
r – λ.(5/4).K-3/4L3/4 = 0
λ.(5/4).K-3/4L3/4 = r
λ = r/((5/4).K-3/4L3/4)
= w – λ.5.(3/4).K1/4L-1/4 = 0
w – λ.(15/4).K1/4L-1/4 = 0
λ.(15/4).K1/4L-1/4 = w
λ = w/((15/4).K1/4L-1/4)
λ = λ
r/((5/4).K-3/4L3/4) = w/((15/4).K1/4L-1/4)
r.(15/4).K1/4L-1/4 = w.(5/4).K-3/4L3/4
kedua ruas dikali 4
r.15.K1/4L-1/4 = w.5.K-3/4L3/4
kedua ruas dibagi 5
r.3.K1/4L-1/4 = w.1.K-3/4L3/4
kedua ruas dikali K3/4.L1/4
r.3.K1L0 = w.K0L1
r.3.K1.1 = w.1.L1
r.3.K = w.L
r.3.K/w = L
L = r.3.K/w
Diketahui r = 10.000 per machine hour, w = Rp.5.000 per man hour
L = 10.000.3.K/5.000
L = 30.000K/5.000
L = 6K
Diketahui Q0 = 1.000 unit
Q = 5.K1/4L3/4
Q = 5. K1/4(6K)3/4
Q = 5. K1/4.63/4K3/4
Q = 5.63/4.K
Q = 19,17K
K = Q/19,17
K = 1.000/19.17
K = 52,17 machine hour
L = 6.K
L = 6. 52.17
L = 313,02 man hour
-
Bila Q’ = 1.100 unit
K = Q/19,17
K = 1.100/19.17
K = 57,38 machine hour
L = 6.K
L = 344,28 man hour
Bila Q” = 1.500
K = Q/19,17
K = 1.500/19.17
K = 78,25 machine hour
L = 6.K
L = 469,5 man hour
-
Rekapitulasi Cost schedule
r = Rp.10.000 per machine hour; w = Rp.5.000 per man hour
|
Q (unit) |
C (rupiah) = r.K + w.L |
Keterangan |
|
1.000 |
2.086.800 |
K = 52,17; L = 313,02 |
|
1.100 |
2.295.200 |
K = 57,38; L = 344,28 |
|
1.500 |
3.130.000 |
K = 78,25; L = 469,5 |
-
Bila cost of capital naik 10%, labor cost naik 5%
r = 10.000 (1 + 10%)
r = 10.000 (1,1)
r = 11.000
w = 5.000 (1+5%)
w = 5.000 (1.05)
w = 5.250
Karena adanya perubahan r dan w, maka kombinasi penggunaan input optimal berubah menjadi:
L = r.3.K/w
L = 11.000.3.K/5.250
L = 33.000K/5.250
L = 6,29K
Sehingga
Q = 5.K1/4L3/4
Q = 5. K1/4(6,2857K)3/4
Q = 5. K1/4.6,28573/4K3/4
Q = 5.6,28573/4.K
Q = 19,85K
K = Q/19,85
Bika Q0 = 1.000
K = 1.000/19,85
K = 50,38
L = 6,29K
L = 6,29. 50,38
L = 316,18
Bila Q’ = 1.100
K = 1.100/19,85
K = 55,42
L = 6,29K
L = 6,29. 55,42
L = 348,59
Bila Q’ = 1.500
K = 1.500/19,85
K = 75,57
L = 6,29K
L = 6,29. 75,57
L = 475,34
r = Rp.11.000 per machine hour; w = Rp.5.250 per man hour
|
Q (unit) |
C (rupiah) = r.K + w.L |
Keterangan |
|
1.000 |
2.214.125 |
K = 50,38; L = 316,18 |
|
1.100 |
2.439.718 |
K = 55,42; L = 348,59 |
|
1.500 |
3.326.805 |
K = 75,57; L = 475,34 |
-
Grafik Cost Function
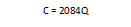
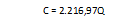
Pada r = 10.000, w = 5.000
C = r.K + w.L
Q = 5.K1/4L3/4
L = 6.K
Q = 5.K1/4L3/4
Q = 5.K1/4.(6K)3/4
Q = 5.63/4.K1/4.K3/4
Q = 5.63/4.K
Q = 19,1682K
K = Q/19,1682
K = 0.0521.Q
C = r.K + w.L
C = 10.000.K + 5.000.6.K
C = 10.000.K + 30.000K
C = 40.000K
C = 40.000.0.0521.Q
C = 2084Q
Pada r = 11.000, w = 5.200
C = r.K + w.L
Q = 5.K1/4L3/4
L = 6,29K
Q = 5.K1/4L3/4
Q = 5.K1/4.(6,29K)3/4
Q = 5.6,293/4.K1/4.K3/4
Q = 5.63/4.K
Q = 19,8590K
K = Q/19,8590
K = 0.05036.Q
C = r.K + w.L
C = 11.000.K + 5.250.6,29.K
C = 11.000.K + 33.022,5K
C = 44.022,5K
C = 44.022,5. 0.05036.Q
C = 2.216,97Q
mohon maaf sebelumnya, pak waktu itu saya menemukan alasan kenapa mc memotong avc dan atc di titik terendah tp dekarang zaya tidak menemukan artikel tersebut. bisakah dijelaskan lagi, karena saya masih penasaran. terimakasih
AC = C/Q, Marginal Cost MC = dC/dQ
Titik minimum kurva AC pada saat turunan pertamanya = 0
d(AC)/dQ = 0
d(A/C)/dQ = 0
d(A.C^-1)/dQ = 0
dC/dQ . Q^-1 + -1.C.Q^-2 = 0
(dC/dQ)/Q – C/Q^2 = 0
( (dC/dQ).Q – C ) / Q^2 = 0
(dC/dQ).Q – C = 0
(dC/dQ).Q = C
dC/dQ = C/Q
MC = AC
terbukti kurva MC memotong kurva AC (Average Cost = Average Total Cost) pada titik minimumnya
begitu juga pada AVC, minimumnya pada saat turunan pertamanya = d(AVC)/dQ = 0
AVC = VC/Q
selanjutnya diselesaikan persamaan
d(AVC)/dQ = 0
d(VC/Q)/dQ = 0
…
d(C)/dQ = VC/Q
terbukti MC memotong pada titik minimum kurva AVC
Suatu perusahaan memproduksi barang A dengan mempekerjakan karyawan. Perusahaan
ini dihadapkan dengan upah tenaga kerja, w = 100.000. Harga barang P adalah
Rp1.000,00. Produktivitas karyawan mengikuti rumus: (ΔQ/ΔL) = 1000*(1/L)0.5
untuk mencari tenaga kerja agar optimal seperti apa ya pak?
Karena P sifatnya ditetapkan = Rp.1000 dan w = 100.000
Optimal kalau laba maksimum, Laba (pi) = Revenue (R) – Biaya (C)
Maksimum saat turunan pertama = 0
Sehingga profit maksimum tercapai pada saat MR = MC
Revenue = P.Q, sehingga MR = P
Cost = FC + VC
FC = Fix Cost
VC = Variabel Cost
Pada soal ini asumsinya variabel cost hanya Labor cost saja maka
Cost = VC
Cost = w.L
MC = d(w.L)/dQ
MC = w.dL/dQ
MC = w/(dQ/dL)
MC = w/MPL
Optimum pada saat MR = MC
karena MR = Px, maka
P = w/MPL
Sehingga Optimum tercapai pada
w/P = MPL
di mana w = wage
P = Price
MPL = dQ/dL
Coba cek persamaan MPL nya apakah benar 1000*(1/L)0.5 <- ? dengan memasukkan w/P = MPL 100.000/1000 = 1000*(1/L)*0.5 100 = 500/L L = 5
terima kasih jawabannya pak.
iya pak itu seharusnya (1/L)^0,5. seharusnya pangkat 0,5. cuma saya masih bingung yang dimasukkan ke persamaannya pak. mengapa menjadi 500/L?
Terima kasih pak
izin bertanya lagi pak kalau MR=P itu kan untuk pasar persaingan sempurna, kalau untuk selain pasar persaingan sempurna seperti apa pak? terima kasih banyak
Karena saya tidak tahu kalau soalnya pangkat
Kalau begitu kita masukkan kembali ke
MPL = 1000*(1/L)^0.5 <- ? dengan memasukkan w/P = MPL 100.000/1000 = 1000*(1/L)^0.5 100 = 1000/L^0.5 L^0.5 = 10 L = 10^2 L = 100
Dalam hali ini berlaku umum, bukan hanya pasar persaingan sempurna saja, karena ini adalah hasil penurunan persamaan untuk mencari optimasi