Supply Function
Oleh: Yohan Naftali
Qsx = f(Px, CP)
CP adalah ceteris paribus/residual/ε
Terdiri dari apa saja CP?
Bermacam-macam, contohnya adalah teknologi
Selain itu sebenarnya Teknologi sudah embodied dalam fungsi produksi
Qsx = α.Kβ.Lγ
α. adalah indek produktifitas
Bila indek efisiensi rendah (dalam hal ini berarti cost rendah, bukan efisiensi-nya yang rendah) maka indek produktifitas tinggi
β dan γ adalah indek elastisitas
Golden Rule

 =
= 
 =
= 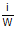


 adalah MRS (Marginal rate of substitution)
adalah MRS (Marginal rate of substitution)

mPK = 
 mPL =
mPL = 
Apabila diketahui fungsi produksi
Q = 2.K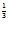 .L
.L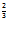
mPK =  = 2.
= 2.  .K
.K .L
.L
mPL =  = 2.
= 2. 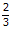 .K
.K .L
.L
Mengingat Golden Rule
 =
=  maka:
maka:
 =
= 
 .K-1.L-1 = 2
.K-1.L-1 = 2
½ K-1.L = 2
L = 4.K
K =  .L
.L
Sampai di sini belum definite, harus dicari berapakah K dan berapakah L
Bila ditentukan budget Bo = 3000
Diketahui bahwa budget adalah perkalian antara tingkat bunga dikalikan dengan Kapital lalu ditambahkan dengan gaji dikalikan Labor sehingga:
Bo = i.K + W.L
Maka:
3000 = 10.K + 5.L
3000 = 10.K + 5.(4.K)
3000 = 10.K + 20.K
3000 = 30.K
K = 100
L = 4.K
L = 4.100
L = 400
Di sini terlihat bahwa L > K sehingga teknologinya adalah Labor Intensive
Unsur Labor Intensive
(1) Produktifitas
Produktifitas L > Produktifitas K
γ > β
2/3 > 1/3
εL > εK
 >
> 
Karenanya disebut Padat Karya (Labor Intensive)
Karena labor 2 kali (2/3 dibagi 1/3) lebih produktif
(2) Ekonomi Price Ratio =  = 2
= 2
Artinya input L 2 kali lebih murah daripada input K
Ditinjau dari 2 sisi maka 2 x 2 = 4 (Lebih efisien pakai L)
Lalu berapa Q yang dihasilkan ?
Q = 2.K .L
.L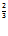
Q = 2.100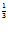 .400
.400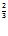
Q = 2.4,64.54.39
Q = 503,81
Dibuat cost schedule
|
Q |
C = Bo = i.K + W.L |
|
|
Qo = 503,81 |
Co = 3000 |
io = 10, Wo = 5 |
Lalu bagaimana bila W berubah menjadi W’ = 7 (io tetap = 10)
Berapakah Q dan C?
 =
= 
½ K-1.L =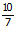
L = 2,86 K
B = i.K + W.L
3000 = 10.K + 7.2,86.K
3000 = 10.K + 20,02.K
3000 = 30,02.K
K = 99,94
L = 2,86.K
L = 2,86.99,94
L = 285,83
Q = 2.K .L
.L
Q = 2.99,94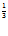 .285,83
.285,83
Q = 2.4,64.43,39
Q = 402,66
Sehingga cost schedule baru menjadi:
|
Q |
C = Bo = i.K + W.L |
|
|
Qo = 503,81 |
Co = 3000 |
io = 10, Wo = 5 |
|
Q‘ = 402,66 |
C‘ = 3000 |
io = 7, Wo = 5 |
Dengan catatan Ceteris Paribus.
Golden Rule
Dari manakah asal golden rule yang menyatakan MR = MC?
πmax => 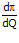 = 0 (lereng = 0)
= 0 (lereng = 0)
π = R – C
R = Revenue
C = Cost
 = 0
= 0
 –
–  = 0
= 0
 =
= 
MR = MC
Bila Px = Pxo = given
Maka
MR ≡  =
=  = Pxo.
= Pxo. 
MR ≡ Pxo
Supply schedule disusun dengan logika
|
Qx |
MC |
Px |
|
|
MC = Pxo |
Pxo |
|
Bila Pxo berubah menjadi Px‘ |
||
|
Qx‘ |
MC’ = Px‘ |
Px‘ |
Supply schedule adalah hubungan antara Qx dengan Px
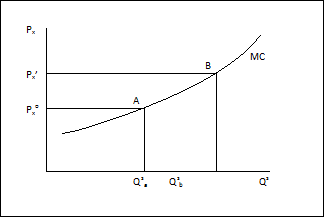

Harga pasar diterima Firm sebagai price taker dan diubah menjadi Qsx.
Bagaimana bila ceteris paribus berubah? (ingat bahwa CP juga dapat berubah)
Bila upah naik akan menggeser kurva MC ke atas (MC’)
Bila teknologi lebih produktif maka akan menggeser kurva MC ke bawah (MC”)


Pxo = ACox + MUo
Pxo↓= ACox↓ + MUo
AC = Unavoidable Financial Burden
MU = Unavoidable instutional (untuk pemilik modal)
Teknologi dan biaya terkait ?
Fungsi produksi dan fungsi biaya ada duality.
Q = f(K, L, T)
Fungsi Produksi Fungsi biaya
(1) TP = Q (1) TC = C
(2) AP = Q/L (Q sebagai numerator) (2) AC = C/Q (Q sebagai denumerator)
(3) MP = dQ/dL (3) MC = dC/dQ
Fungsi produksi merupakan invers dari fungsi biaya
AC = =
=  =
= 
MP = 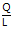
AC = 
MC = 
Sehingga cost function ≡ mirror reflection dari production function


SOP Optimization
Maximization sebagai objective ≈ Minimization sebagai objective
Maksimumkan Qx
Objective Qx = f(K, L, T)
Constraint Bo = Po.K + Wo.L
Optimum G = Objective – λ.Constraint
Minimumkan B
Cari kombinasi K dan L sedemikian rupa sehingga least cost
Objective B = i.K + Wo.L
Constraint Qx = f(K, L, T)
Optimum G = Objective – λ.Constraint

Leave a Reply