Elastisitas (ε)
Oleh: Yohan Naftali, ST, MM
Credit to : Prof Dr H Sudarsono
Pada bagian ini akan dijelaskan mengenai konsep elasitsitas dan kegunaan elasitisitas. Elastisitas berguna sekali untuk pengusaha dalam mengambil kebijakan harga yang tepat karena perubahan harga dan perubahan permintaan akan mempengaruhi besarnya penjualan, dan pada akhirnya akan mempengaruhi laba.
Asumsi dalam elastisitas adalah perubahan harga akan mempengaruhi perubahan permintaan. Harga di sini tidak terbatas dengan harga barang tersebut akan tetapi juga harga barang lainnya. Pada keadaan normal, apabila harga sebuah mobil merk X turun, maka permintaan akan kendaraan tersebut akan meningkat. Pada kejadian yang sama bila harga pesaing mobil merk X naik, maka hal ini dapat menyebabkan permintaan mobil merk X akan naik. Mobil pesaing ini disebut barang subtitusi. Di samping itu bila harga barang pelengkap/komplementer (misalkan bahan bakar) turun maka permintaan mobil merk X juga akan naik.
Elastisitas (ε) adalah indek yang menggambarkan derajat kepekaan perubahan harga bila terjadi perubahan permintaan. Indek elastisitas diketahui dengan menghitung persentase perubahan permintaan terhadap persentase perubahan harga. Secara umum bentuk matematika elastisitas adalah:

Ada dua jenis elastisitas yaitu elastisitas busur (arc elasticity) dan elastisitas titik (point elasticity). Elastisitas busur adalah derajat kepekaan perubahan harga di antara 2 kejadian perubahan permintaan, dengan kata lain elastisitas busur adalah elastisitas di antara 2 titik. Apabila jarak antara 2 titik tersebut sangat kecil sekali (mendekati 0) maka elastisitas busur menjadi elastisitas titik, sehingga dapat dikatakan elastisitas titik adalah derajat kepekaan perubahan harga pada suatu titik perubahan permintaan. Elastisitas titik lebih relevan untuk digunakan dalam penentuan kebijakan harga daripada elastisitas busur. Akan tetapi di sini perlu memahami konsep mengenai elastisitas busur sebagai dasar penurunan rumus elastisitas titik.
Untuk menjelaskan konsep elastistas busur diilustrasikan dengan suatu barang X yang memiliki permintaan sebanyak 15 satuan pada saat harga Rp. 10. Pada saat harga barang X diturunkan menjadi Rp. 8 ternyata barang X mengalami peningkatan permintaan menjadi 25 satuan. Informasi ini dapat digunakan untuk menghitung elastisitas busur. Untuk mempermudah pemahaman, informasi di atas digambarkan pada grafik berikut ini. Dengan mengetahui 2 titik (A dan B) dapat dibuat kurva permintaan (Dx).
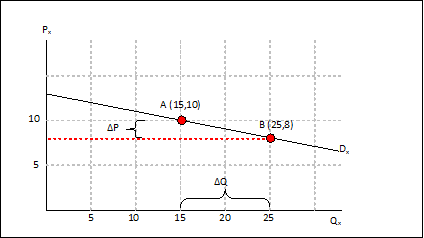

Dari grafik terlihat bahwa dengan adanya penurunan harga maka permintaan akan naik. Apabila ditaris garis lurus antara titik A dan titik B maka didapatkan sebuah kurva permintaan (Dx) dengan slope yang menurun. Perubahan harga ditunjukkan dengan jarak antara 2 titik A dan B pada sumbu vertikal sebesar ΔP. Perubahan permintaan juga ditunjukkan dengan jarak antara 2 titik A dan B pada sumbu horisontal sebesar ΔQ.
Perubahan Permintaan (ΔQ) dihitung dengan cara mencari selisih permintaan antara 2 titik. Hasil perhitungan menunjukan bahwa setelah perubahan harga terjadi kenaikan permintaan sebesar 10 satuan.
ΔQ = QB – QA
ΔQ = 25 – 15 = 10 (permintaan naik sebesar 10 satuan)
Dalam hal menghitung elastisitas busur, maka untuk menentukan permintaan (Q) adalah dengan menghitung nilai rata-rata permintaan. Nilai rata-rata didapat dengan menjumlahkan kedua permintaan dan membaginya dengan dua.
Q = 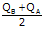
Q = 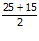
Q = 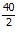
Q = 20 (rata-rata permintaan adalah 20 satuan)
Setelah mengetahui perubahan permintaan dan rata-rata permintaan, selanjutnya dapat dihitung persentase perubahan permintaan (%ΔQ) dengan membagi perubahan permintaan dengan rata-rata permintaan.
%ΔQ = 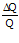
%ΔQ = 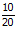
%ΔQ = 0.5 = 50% (perubahan permintaan sebesar 50%)
Selanjutnya menghitung perubahan harga dengan cara mencari selisih harga sesudah perubahan harga dan sebelum perubahan harga. Hasil perhitungan menunjukkan harga mengalami penurunan sebesar Rp. 2.
ΔP = PB – PA
ΔP = 8 – 10 = -2 (harga turun sebesar Rp. 2)
Dengan cara yang sama, dalam hal menghitung elastisitas busur maka untuk menghitung harga yang digunakan (P) adalah dengan menghitung nilai rata-rata permintaan. Rata-rata didapatkan dengan menjumlahkan kedua nilai harga lalu membaginya dengan 2.
P = 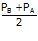
P = 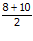
P = 
P = 9 (rata-rata harga adalah sebesar Rp. 9)
Setelah mengetahui perubahan harga dan rata-rata harga maka dapat dihitung persentase perubahan harga. Persentase perubahan harga (%ΔP) dihitung dengan cara membagi perubahan harga dengan rata-rata harga.
%ΔP = 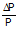
%ΔP = 
%ΔP = 0.2222 = 22,22% (perubahan harga sebesar 22,22%)
Setelah persentase perubahan permintaan dan persentase perubahan harga diketahui maka dapat dihitung elastisitas busur. Elastisitas busur dapat dihitung dengan cara membagi persentase perubahan permintaan dan persentase perubahan harga.
ε = 
ε = 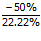
ε = – 2,25
Elastisitas busur pada contoh ini adalah sebesar -2.25, tanda negatif (-) menunjukkan bahwa arah perubahan harga berlawanan arah dengan perubahan permintaan, sehingga bila harga diturunkan maka permintaan akan naik, begitu juga sebaliknya bila harga dinaikkan maka permintaan akan turun. Angka 2,25 menunjukan magnitude dari elastisitas, semakin tinggi magnitude dari elastisitas menunjukkan semakin tingginya derajat kepekaan, dalam grafik ditunjukkan dengan garis yang semakin mendatar. Apabila magnitude elastisitas lebih kecil dari 1 maka disebut inelastik, sedangkan bila nilai elastisitas sama dengan 1 disebut unitary.
Setelah mempelajari contoh perhitungan elastisitas busur, maka dapat dirangkumkan persamaan khusus untuk menghitung elastisitas busur. Persamaan ini merupakan penurunan dari persamaan elastisitas yang umum dengan jalam mensubtitusi komponen dalam persamaan dengan persamaan khusus menghitung elastisitas busur.
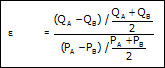
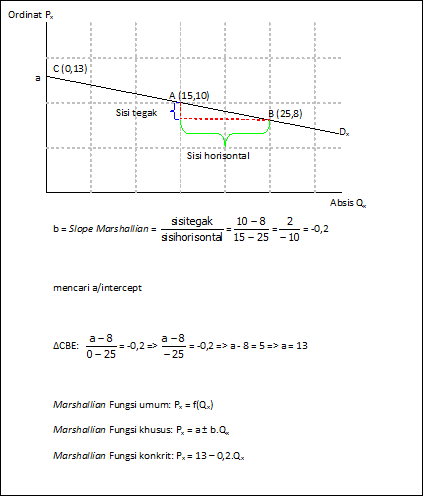
Selain elastisitas busur, dapat dihitung juga elastisitas titik. Elastisitas titik dapat dihitung dengan penurunan rumus berikut ini.
εp = 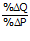
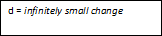 εp =
εp = 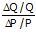
εp = 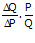
karena perbandingan antara  =
=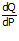 maka didapatkan,
maka didapatkan,
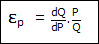

Dari penurunan persamaan di atas ditunjukkan bahwa untuk menghitung elastisitas titik adalah dengan mengkalikan slope pada kurva permintaan dengan harga, lalu membaginya dengan jumlah permintaan. Perlu diperhatikan slope yang digunakan adalah slope pada fungsi permintaan versi walras (Q = f(P)).
Dengan contoh sebelumnya dapat dihitung juga elastisitas pada titik A dan elastisitas pada titik B. Sebelum menghitung elastisitas titik maka perlu dicari dahulu slope persamaan dari kurva permintaan Q=f(P).

εp = 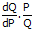
εpA = -5.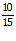 = -5.
= -5. 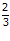 = –
= –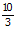 = -3.3
= -3.3
εpB = -5.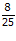 = –
= –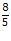 = -1.6
= -1.6
Dari contoh ini bila dibuat hasilnya dijadikan bentuk tabular maka akan menghasilkan tabel seperti berikut ini. Dari data ini terlihat bahwa dengan penurunan harga maka magnitude elastisitas akan turun.
|
Px |
Qx |
ε |
|
10 |
15 |
-3,3 |
|
8 |
25 |
-1,6 |
Bila elastisitas sudah dihitung, maka informasi ini penting untuk menentukan kebijakan harga. Penjelasan berikut ini menjabarkan bagaimana hubungan elastisitas dan kebijakan harga. Dalam menentukan kebijakan harga yang diambil ada 3 pilihan yang dapat diambil yaitu:
- menaikkan harga.
- menurunkan harga.
- tidak merubah harga.
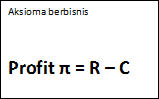 Dengan kondisi yang sama seperti contoh sebelumnya, maka bila diketahui Pxo = 9, ditanyakan kebijakan harga mana yang akan diambil oleh pengusaha? Apakah akan menaikkan harga, apakah pengusaha akan menurukan harga? Atau tidak mengubah harga? Untuk mengetahuinya perlu dipahami dahulu mengenai aksioma berbisnis yaitu meningkatkan laba/profit. Profit (π) didapatkan dari mengurangi pendapatan (revenue) dengan biaya (cost). Bila diinginkan profit (π) naik maka pendapatan (R) harus dinaikkan (dalam hal ini diasumsikan tidak ada data biaya, atau perubahan biaya). Pendapatan (R) didapatkan dari harga (P) dikalikan dengan jumlah penjualan (Q).
Dengan kondisi yang sama seperti contoh sebelumnya, maka bila diketahui Pxo = 9, ditanyakan kebijakan harga mana yang akan diambil oleh pengusaha? Apakah akan menaikkan harga, apakah pengusaha akan menurukan harga? Atau tidak mengubah harga? Untuk mengetahuinya perlu dipahami dahulu mengenai aksioma berbisnis yaitu meningkatkan laba/profit. Profit (π) didapatkan dari mengurangi pendapatan (revenue) dengan biaya (cost). Bila diinginkan profit (π) naik maka pendapatan (R) harus dinaikkan (dalam hal ini diasumsikan tidak ada data biaya, atau perubahan biaya). Pendapatan (R) didapatkan dari harga (P) dikalikan dengan jumlah penjualan (Q).
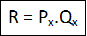
Karena Pxo sudah ditentukan, dan fungsi permintaan sudah diketahui maka dapat dicari jumlah permintaan (Qx) pada harga Pxo = 9. Untuk menghitung ada 2 cara yaitu dengan menggunakan fungsi permintaan versi Marshall (P = f(Q)) atau menggunakan fungsi permintaan Walras (Q = f(P)).

Perhitungan menghasilkan bahwa permintaan akan sebesar 20 satuan pada harga Rp 9. Dari perhitungan berikut ini diketahui bahwa perolehan (R) yang diperoleh adalah sebesar Rp. 180.
R = Pxo.Qx
R = 9 x 20
R = 180
Untuk mengetahui apakah harus menurunkan atau menaikkan harga. Maka dapat dicoba menghitung perolehan (R) bila harga diturunkan menjadi Px‘, misal harga Px‘ = 8. Alternatifnya adalah menghitung R bila harga dinaikkan menjadi Px” = 10. Karena pada harga Px‘ = 8 dan Px” = 9, jumlah permintaan (Q) sudah diketahui maka dapat langsung dihitung perolehannya (R) dengan cara mengkalikan masing masing harga dengan jumlah permintaannya.
Hasil perhitungan perolehan (R) ditulis dalam tabel berikut ini:
|
Px |
Qx |
ε |
R |
|
10 |
15 |
-3,3 |
10 x 15 = 150 |
|
9 |
20 |
-5.(9/20) = -2,25 |
9 x 20 = 180 |
|
8 |
25 |
-1,6 |
8 x 5 = 200 |
Karena perolehan (R) pada saat harga diturunkan lebih besar daripada harga Pxo = 9 maka, pada saat harga Pxo = 9, pengusaha akan lebih untung bila menurunkan harga. Dari tabel di atas terlihat juga pada saat magnitude elastisitas turun, perolehannya (R) semakin meningkat. Sampai di sini belum diketahui apakah pada saat magnitude semakin kecil akan menghasilkan perolehan yang lebih besar lagi.
Selanjutnya dicoba untuk menurunkan harga yang mungkin menghasilkan magnitude elastisitas yang cukup kecil. Oleh karena itu bila dicoba pada harga Pxo = 2, berapa revenue yang didapatkan. Di sini akan ditanyakan juga kebijakan apa yang akan diambil pengusaha? Untuk mengetahuinya harus dihitung lagi perolehan (R) pada saat harga Px‘ = 3 (harga dinaikkan) dan Px” = 1 (harga diturunkan).
Pada saat Pxo = 2
Qx = 65 – 5.Px
Qx = 65 – 5.2
Qx = 65 – 10
Qx = 55
R = Pxo. Qx
R = 2.55
R = 110
Pada saat Pxo = 3
Qx = 65 – 5.Px
Qx = 65 – 5.3
Qx = 65 – 15
Qx = 50
R = Pxo. Qx
R = 3.50
R = 150 (Revenue naik)
Pada saat Pxo = 1
Qx = 65 – 5.Px
Qx = 65 – 5.1
Qx = 65 – 5
Qx = 60
R = Pxo. Qx
R = 1.60
R = 60 (Revenue turun)
Hasil perhitungan disajikan dalam bentuk tabular pada tabel berikut ini:
|
Px |
Qx |
ε |
R |
|
3 |
50 |
-5.(3/50) = -0,3 |
150 |
|
2 |
55 |
-5.(2/55) = -0,18 |
110 |
|
1 |
60 |
-5.(1/60) = -0,08 |
60 |
Dari hasil perhitungan menunjukkan bahwa pengusaha akan lebih untung bila menaikkan harga pada saat Pxo = 2, karena menghasilkan revenue yang lebih tinggi. Di sini diperlihatkan bahwa dengan penurunan magnitude elastisitas justru terjadi penurunan perolehan.
Lalu apa gunanya elastisitas (ε) ?
Untuk mengetahuinya, tabel sebelumnya disusun kembali menjadi satu tabel. Tabel berikut ini menunjukkan bahwa adanya perbedaan hubungan antara indek elastisitas di atas 1 dan indek elastisitas di bawah 1.
|
Px |
Qx |
ε |
R |
|
10 |
15 |
-3,3 |
150 |
|
9 |
20 |
-2,25 |
180 |
|
8 |
25 |
-1,6 |
200 |
|
3 |
50 |
-0,3 |
150 |
|
2 |
55 |
-0,18 |
110 |
|
1 |
60 |
-0,08 |
60 |
Dari contoh di atas dapat disimpulkan bahwa
Bila index elastisitas > 1 (elastik) maka akan menguntungkan bila harga diturunkan karena Revenue yang didapat lebih tinggi
ε > 1 => (P↓ → R↑)
Bila index elastisitas < 1 (inelastik) maka akan menguntungkan bila harga dinaikkan karena revenue yang didapat lebih tinggi
ε < 1 => (P↑ → R↑)
Jadi index elastisitas juga dapat untuk menentukan kebijakan harga, fungsi permintaan dimanfaatkan pengusaha untuk mengambil keputusan yang tepat dalam kebijakan harga. Perlu diingat dalam elastisitas harus dibedakan antara sign of elasticity dan magnitude of elasticity, indek elastisitas yang dimaksud oleh pernyataan di atas adalah magnitude-nya


Contoh untuk ε = -2,25,
tandanya negatif karena ε (-) < 0
magnitude-nya ε (2,25) > 1 artinya elastik.
Lebih jauh dengan fungsi permintaan dan elastisitas
Pada pembahasan sebelumnya, hanya dibicarakan mengenai elastisitas harga sendiri (own price elasticity), sedangkan elastisias sendiri ada bermacam-macam, karena perubahan permintaan tidak hanya dipengaruhi oleh perubahan harga sendiri akan tetapi juga dipengaruhi oleh harga lainnya. Pada prinsipnya elastisitas adalah derajat perubahan suatu faktor terhadap perubahan permintaan. Elastisitas dihitung dengan melakukan turunan/derivasi parsial fungsi permintaan. Untuk menentukan apakah suatu jenis barang adalah barang komplementer atau barang subtitusi, dapat dilihat tanda dari indek elastisitasnya. Bila tandanya negatif, maka barang tersebut merupakan barang komplementer, sedangkan bila tandanya positif, barang tersebut merupakan barang subtitusi, dengan syarat ceteris paribus.
Fungsi umum permintaan:
Qdx = f(Px, Pk, Ps, M, ε)
Px = harga barang
Pk = harga barang komplementer
Ps = harga barang subtitusi
M = income
ε = disturbance term error
(bedakan dengan ε elastisitas)
Berikut ini adalah rangkuman persamaan untuk menghitung elastisitas.
εPx = 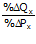 = own price elasticity => tandanya negatif (εPx < 0)
= own price elasticity => tandanya negatif (εPx < 0)
εPk = 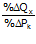 = cross elasticity => tandanya negatif (εPk < 0) karena k K
= cross elasticity => tandanya negatif (εPk < 0) karena k K
x
εPs = 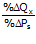 = cross elasticity => tandanya positif (εPk > 0)
= cross elasticity => tandanya positif (εPk > 0)
εm = 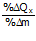 = income elasticity
= income elasticity
Sedangkan untuk disturbance term error, termasuk di dalamnya adalah selera (taste). Elastisitas pada faktor lainnya sulit/tidak dapat dihitung karena sifatnya unquantifiable, unmeasureable, unobservable, unrecordable.
Perilaku konsumen digambarkan dalam persamaan fungsi permintaan, secara umum dan ceteris paribus, perilaku konsumen dapat disimpulkan sebagai berikut:
-
Permintaan suatu barang cenderung naik apabila harga barang tersebut mengalami penurunan.
-
Permintaan suatu barang cenderung naik apabila harga barang pelengkapnya (komplementer) mengalami penurunan.
-
Permintaan suatu barang cenderung naik apabila harga barang subtitusinya mengalami kenaikan.
-
Dalam hubungannya dengan perubahan tingkat pendapatan (income), maka barang dapat dibagi menjadi tiga kelompok, yaitu barang superior, barang inferior, dan barang netral. Permintaan akan barang superior cenderung naik apabila tingkat pendapatan naik. Permintaan akan barang inferior cenderung turun apabila tingkat pendapatan naik. Permintaan akan barang netral tidak mengalami perubahan walaupun terjadi perubahan tingkat pendapatan.
Leave a Reply