Kepuasan
Kapan mencapai kepuasan? Apakah ada batasnya?
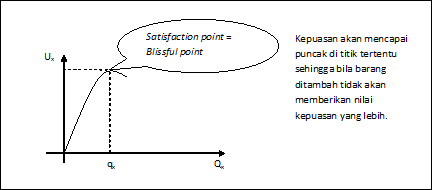
Dengan mengetahui bahwa kepuasan itu ada batasnya, serta dari studi perilaku konsumen yang menunjukkan bahwa kepuasan pada penambahan barang pertama lebih tinggi daripada tingkat kepuasan pada barang selanjutnya, maka grafik marginal utility akan semakin mengecil, sampai pada suatu titik tertentu di mana penambahan kepuasan bernilai nol pada saat penambahan barang.
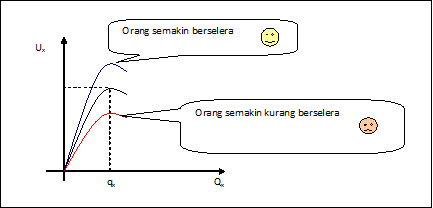
Marshall = pendekatan parsial
Walras = pendekatan general
Fungsi umum dari fungsi permintaan (pendekatan Walras)
Qdx = f(Px, Pk, Ps, M, ε)
Fungsi khusus (non linear, sifatnya multiplikatif)
Qdx = a.Pxα.Pkβ.Psγ.Mδ.εη
Px = harga barang
Pk = harga barang komplementer
Ps = harga barang subtitusi
M = income
ε = disturbance term error/error term/residual term/sisa dianggap ceteris paribus
(dibaca epsilon), subtansinya given, tertentu, “tetap”, diberi notasi naught (nol kecil) sebagai superscript.
Ceteris paribus selalu dengan catatan bahwa hal-hal lainya tetap (tidak berubah/tidak mempengaruhi perubahan dependent variabel) akan tetapi ceteris paribus itu bisa berubah.
α = elasticity index
β = cross elasticity index
γ = cross elasticity index
δ = income elasticity index of demand function of x
η = (dibaca eta) index disturbance term error
Fungsi khusus sifatnya inspearable (tidak bisa dipisahkan)
Karena sifatnya yang non linear, maka untuk mempermudah analisis dilinearkan dengan transformasi logaritma mengunakan logaritma natural
ln Qdx = ln a + α.ln Px + β.ln Pk + γ.ln Ps + δ.lnM
ε
= not available.
Sehingga persamaan dapat disederhanakan menjadi:
Y = a + α.X1 + β.X2 + γ.X3 + δ.X4
Keterangan:
Y = ln Qdx
X1 = ln Px
X2 = ln Pk
X3 = ln Ps
X4 = ln M
Kemudian dalam tabel data, masing masing data dicari nilai logaritma naturalnya (ln).
|
Qdx |
Y = ln Qdx |
Px |
X1 = ln Px |
Pk |
X2 = ln Pk |
Ps |
X3 = ln Ps |
M |
X4 = ln M |
|
a |
ln a |
d |
ln d |
g |
ln g |
j |
ln j |
l |
ln l |
|
b |
ln b |
e |
ln e |
h |
ln h |
k |
ln k |
m |
ln m |
|
c |
ln c |
f |
ln f |
i |
ln i |
k |
ln k |
z |
ln z |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
n |
ln n |
o |
ln o |
p |
ln p |
q |
ln q |
r |
ln r |
|
Σy |
Σx1 |
Σx2 |
Σx3 |
Σx4 |
Selanjutnya diselesaikan dengan cara mencari koefisien pada persamaan linear.
Cara mencari koefisien dalam fungsi linear
Bila diketahui y = f(x1)
y = c + α.x1
dari data dibuat tabel dahulu
|
n |
y (Px) |
x1 (Qdx) |
y.x1 |
x1. x1 = (x12) |
|
n1 |
5 |
3 |
5×3=15 |
3×3=9 |
|
n2 |
1 |
4 |
1×4=4 |
4×4=16 |
|
n=2 |
Σy=5+1=6 |
Σx1=3+4=7 |
Σy.x1=15+4=19 |
Σx12=9+16=25 |
buat standard normal equations
(1) Σy = n.C + α .Σx1
(2) Σy.x1 = C. Σx1 + α .Σx12
Sehingga
(1) 6 = 2.C + α .7
(2) 19 = C. 7 + α .25
Untuk mencari C dan α
Cari dahulu invers dari matrik 
Mencari invers matrik dengan metode eliminasi Gauss-Jordan
Menggunakan sifat [A.I] = [I.A-1]
A adalah matrik yang akan dicari invers-nya
I adalah matrik identitas, dalam hal ini adalah matrik bujursangkar yang dimensinya sama dengan matrik A dan memiliki nilai 1 pada setiap sel yang nomer baris dan kolomnya sama, sedangkan untuk sel lainnya bernilai 0
Sehingga :
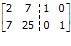
Bagi baris pertama dengan 2 supaya baris 1 kolom 1 menjadi 1
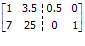
Kurangi baris pertama dengan 7 kali baris 1 supaya baris 2 kolom 1 menjadi 0
Bagi baris kedua dengan 0.5 supaya baris 2 kolom 2 menjadi 1
Kurangi baris 1 dengan 3.5 kali baris 2 supaya baris 1 kolom 2 menjadi 0
Sehingga invers matrik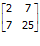 
adalah 
Sehingga persamaan menjadi:
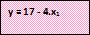
Sehingga
Bandingkan hasilnya dengan cara pengerjaan menggunakan grafik seperti dijelaskan pada bagian terdahulu.
Metode penyelesaian ini bukan satu-satunya cara, masih banyak cara lainnya, hal ini dapat di pelajari di dalam mata kuliah aljabar linier.
Standard normal equations
y = f(x1) memiliki 2 unknown (C dan α)
Dibutuhkan 2 persamaan yang dibentuk dengan:
(1) Σy = n.C + α .Σx1
(2) Σy.x1 = C.Σx1 + α .Σx12
y = f(x1, x2) memiliki 3 unknown (C, α, dan β)
Dibutuhkan 3 persamaan yang dibentuk dengan:
(1) Σy = n.C + α .Σx1
(2) Σy.x1 = C.Σx1 + α .Σx12 + β.Σx1.x2
(2) Σy.x2 = C.Σx2 + α .Σx1.x2 + β.Σx22
y = f(x1, x2, x3) memiliki 4 unknown (C, α, β, dan γ)
Dibutuhkan 4 persamaan yang dibentuk dengan:
(1) Σy = n.C + α .Σx1 + β.Σx2 + γ.Σx3
(2) Σy.x1 = C.Σx1 + α .Σx12 + β.Σx1.x2 + γ.Σx1.x3
(3) Σy.x2 = C.Σx2 + α .Σx1.x2 + β.Σx22 + γ.Σx2.x3
(4) Σy.x3 = C.Σx3 + α .Σx1.x3 + β.Σx2.x3
+ γ.Σx32
y = f(x1, x2, x3, x4) memiliki 5 unknown (C, α, β, γ, dan δ)
Dibutuhkan 5 persamaan yang dibentuk dengan:
(1) Σy = n.C + α .Σx1 + β.Σx2 + γ.Σx3 + δ.Σx4
(2) Σy.x1 = C.Σx1 + α .Σx12 + β.Σx1.x2 + γ.Σx1.x3 + δ.Σx1.x4
(3) Σy.x2 = C.Σx2 + α .Σx1.x2 + β.Σx22 + γ.Σx2.x3 + δ.Σx2.x4
(4) Σy.x3 = C.Σx3 + α .Σx1.x3 + β.Σx2.x3
+ γ.Σx32 + δ.Σx3.x4
(5) Σy.x4 = C.Σx4 + α .Σx1.x4 + β.Σx2.x4
+ γ.Σx3.x4 + δ.Σx42
Dan seterusnya …
|
No data |
y |
x1 |
x2 |
x3 |
x4 |
y.x1 |
y.x2 |
Σy.x3 |
y.x4 |
x12 |
x1.x2 |
x1.x3 |
x1.x4 |
|
1 |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
2 |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
3 |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
n |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
Total |
Σy |
Σx1 |
Σx2 |
Σx3 |
Σx4 |
Σy.x1 |
Σy.x2 |
Σy.x3 |
Σy.x4 |
Σx12 |
Σx1.x2 |
Σx1.x3 |
Σx1.x4 |
|
No data |
x22 |
x2.x3 |
x2.x4 |
x32 |
x3.x4 |
Σx42 |
|
1 |
||||||
|
2 |
… |
… |
… |
… |
… |
… |
|
3 |
… |
… |
… |
… |
… |
… |
|
… |
… |
… |
… |
… |
… |
… |
|
n |
… |
… |
… |
… |
… |
… |
|
Total |
Σx22 |
Σx2.x3 |
Σx2.x4 |
Σx32 |
Σx3.x4 |
Σx42 |
Leave a Reply