BEHAVIOR OF THE FIRM

 

 

Kalau pada bagian sebelumnya diperlajari perilaku konsumen dengan pendekatan Demand Function (Fungsi permintaan) maka perilaku Firm sebagai produsen dipelajari dengan pendekaran Supply Function.

 

Referensi buku : Pyndick & Rubenfeld (Microeconomics)

 

Definisi Supply Function:

yaitu sebuah fungsi yang menggambarkan kuantitas barang yang ditawarkan dengan harganya (P_x dan Q_x), berbagai-bagai P^s_x pada berbagai-bagai P^s_x

 

Supply function:

dinyatakan dalam persamaan matematika (model Walras)

 

Q^s_x = f(P_x)

 

Menurut Marshall P_x = f(Q^s_x) (Pendekatan grafikal)

 

Pendekatan supply function:

(1) Production function

(2) Cost function

 

Fungsi produksi (Production function)

Definisi: fungsi yang menggambarkan hubungan teknis antara input dan output

Dalam persamaan matematika dinyatakan sebagai:

 

Q^s_x = f(input)

 

Faktor input disederhanakan menjadi 3 kategori saja yaitu

(1) K = Kapital

(2) L = Labor

(3) T = Teknologi

 

Firm awalnya adalah sebagai produsen, lalu menjadi seller sejumlah Q^s_x.

Peran firm sebagai produsen adalah menentukan banyaknya kuantitas barang yang akan diproduksi.

Masalah utama ekonomi

What : Q^d_x (demand) optimum?

How : input -> metode kombinasi input (K*, L*, T^o)

For Whom ?

 

 

 

 

T dianggap sebagai ceteris paribus, T dapat berubah in the very long run

Sehingga fungsi supply pada very long run

 

Q^s_x = f(K, L, T)

Pada medium long run

 

Q^s_x = f(K, L)

 

 

 

 

Fungsi pada long run tidak digunakan karena in the long run we’re all dead (Keynes)

 

Kapan Long Run /Short Run ?

 

Menurut akuntansi short run itu < 1 tahun, Long Run > 1 tahun

 

Dalam ekonomi:

 

Short Run =     Jangka waktu yang sedemikian singkatnya sehingga pengusaha tidak mempunyai waktu yang cukup untuk merubah inputnya

 

Long Run =    Jangka waktu yang cukup panjang sehingga pengusaha mempunyai waktu yang cukup untuk merubah inputnya

 

Bagaimana production function pada short run?

 

Production Function (Short Run)

 

Q^s_x = f(L)

 

Dalam grafik

 

 

 

 

 

 

 

 

 

 

 

Pada fungsi produksi dikenal

(1) MPL

(2) APL

 

Jadi issue dalam fungsi produksi adalah mencari kombinasi L*

 

Berapa L* ?

 

 

L* adalah L yang Optimal

 

Bagaimana mencarinya?

 

Untuk mencarinya menggunakan golden rule

 

P_L = V.mP_L

 

P_L = Price of labor = Wage = W

mP_L = =

 

V = Value (nilai pasar)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

         (-)            (+)

     Upah         Produktifitas

        W         V.mP_L

 

 

        Harus seimbang

Sehingga

Persamaan golden rule P_L = V.mP_L menjadi:

 

W^o = P_x.mP_L

 

 

W^o = given => in the neighborhood of market price

Karena di sini diasumsikan firm sebagai price taker (bukan pasar monopoli)

 

Fungsi produksi pada persamaan Q^s_x = f(L) adalah fungsi produksi secara umum, sedangkan fungsi khususnya adalah:

 

Q = aL – bL²

 

Sebagai contoh fungsi produksi secara konkrit adalah:

 

 

 

mP_L = 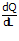adalah turunan pertama dari fungsi induk (first derivative)

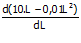= = 10 – 0,02L

 

W^o dan P_x^o (harga labor dan nilai pasar sudah ditentukan)

 

Pada contoh ini misalkan harga labor W^o = 5 dan P_x^o = 10, maka dengan golden rule

W^o = P_x.mP_L

5 = 10.mP_L

5 = 10.(10-0,02L)

5 = 100 – 0,2L

0,2L = 95

L* = 475

Setelah L* diketahui, dapat dihitung Q*

Q* = 10L* – 0,01.L²

Q* = 10 x 475 – 0,01 x 475²

Q* = 4750 – 2256,25

Q* = 2493,75

 

 

 

 

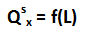
Fungsi biaya (Cost function)

Diderivasi dari fungsi produksi (production function)

Kalau fungsi produksi adalah Q = f(L), maka fungsi biaya adalah:

C = f(Q)

 

Cost structure terdiri dari

(1) fixed cost

(2) variable cost

 

 

 

 

 

 

Adakah cost yang “tidak dapat dihitung” ?

Kalau “tidak dihitung” ada (bukan tidak dapat dihitung)

Contohnya :     Tukang bakso ada biaya yang tidak dihitung yaitu implicit cost yang berasal dari gaji untuk dirinya sendiri, pembantunya (karena anak sendiri), dll.

 

Variable cost (VC, biaya variabel) adalah biaya yang besarnya tergantung volume produksi

Fixed cost (FC, biaya tetap) adalah biaya yang besarnya tidak tergantung dengan volume produksi

 

C = FC + VC

 

Rekapitulasi C = f(Q) pada contoh sebelumnya ketika W^o = 5 pada fungsi:

 

Q = 10.L – 0,01.L²

 

 

Untuk membuat grafik harus ada 2 titik, maka coba bila W = 6.

 

Bagaimana bila W naik menjadi 6.

W^o = P_x.mP_L

6 = 10.mP_L

6 = 10.(10-0,02L*₂)

6 = 100 – 0,2L*₂

0,2L*₂ = 94

L*₂ = 94/0,2

L*₂ = 470

 

Q*₂ = 10L*₂ – 0,01.L*₂²

Q*₂ = 10 x 470 – 0,01 x 470²

Q*₂ = 4700 – 2209

Q*₂ = 2491

 

Bagaimana bila W naik menjadi 10.

W^o = P_x.mP_L

10 = 10.mP_L

10 = 10.(10-0,02L*₃)

10 = 100 – 0,2L*₃

0,2L*₃ = 90

L*₃ = 90/0,2

L*₃ = 450

 

Q*₃ = 10L*₃ – 0,01.L*₃²

Q*₃ = 10 x 450 – 0,01 x 450²

Q*₃ = 4500 – 2025

Q*₃ = 2475

 

Dibuat dalam tabel

Cost Schedule

 

ΔQ = 2475 – 2493,75 = -18.75

ΔC = 4500 – 2375 = 2125

 

Dengan perubahan ΔW akan merubah ΔQ

Grafik fungsi biaya (cost function) dianggap linear

 

 

 

 

 

 

 

 

 

 

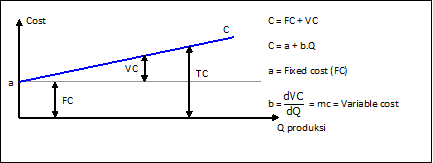
Pada kenyataannya variabel cost itu bentuknya tidak linier sehingga grafiknya seperti di bawah ini:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Graphical Average Function

 

AC = Average Total Cost =

AVC = Average Variable Cost =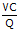

AFC = Average Fixed Cost =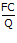

MC = Marginal Cost =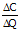

 

 

 

 

 

 

 

 

 

 

 

Setelah didapatkan AFC dan AVC, bisa digambarkan garis AC dengan cara superposisi antara garis AFC dan garis AVC.

 

AC = AFC + AVC

 

Letak garis AC di atas garis AVC, jarak garis AC dari garis AVC adalah sama dengan jarak sumbu horisontal ke garis AFC.

 

 

 

 

Setelah berhasil menggambar garis AVC, AFC, dan AC, maka dapat digambarkan garis MC (Marginal Cost).

 

 

Kenapa MC memotong pada titik AC minimum?

 

Pada titik minimum AC maka = 0 karena lereng/slope datar.

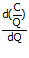= 0

= 0

 

Q^-1 + -1.C.Q^-2 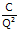= 0

 

– = 0

 

= 0

 

.Q – C = 0

 

.Q = C

 

=

 

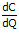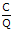
MU = AC (ingat bahwa AC = , dan MU = )

 

Terbukti bahwa garis MU memotong garis AC pada titik minimum AC

 

 

Apakah garis MU juga memotong garis AVC pada titik minimumnya?

 

Pada titik minimum AVC maka 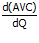= 0 karena lereng/slope datar.

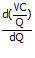= 0

= 0

 

Q^-1 + -1.VC.Q^-2 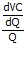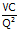= 0

 

– = 0

 

= 0

 

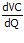.Q – VC = 0

 

.Q = VC

 

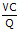= (Ingat bahwa bahwa AVC = , dan MU = )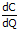

 

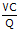= (Karena C = AFC + VC, sehingga VC = C – AFC)

 

– =

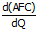– 0 =

 

=

 

Terbukti bahwa garis MU memotong garis AVC pada titik minimumnya.

Turunan (Derivative)

 

Apa itu turunan (derivative)?

Sama saja dengan marginal dalam ekonomi, pada y=f(x), dibaca y sama dengan fungsi x, maka turunan y terhadap x yaitu perbandingan perubahan y setiap perubahan x, dengan x adalah kecil sekali (mendekati 0, tapi bukan 0)

Turunan dilambangkan dengan ( ini apabila kita mau menurunkan fungsi y pada x), boleh saja ditulis bila kita ingin menurunkan fungsi C pada Q, artinya perubahan C setiap perubahan Q

 

Contohnya?

Misal kita punya fungsi y = 5x², maka turunannya terhadap x (dinotasikan dengan )

adalah:

 

= 2.5.x^(2-1)

 

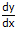= 10.x⁽¹⁾

 

Lihat bahwa 2 berasal dari pangkatnya, dan pangkatnya dikurangi dengan 1.

 

Lalu kalau fungsinya berbentuk y = 5x²
– 10, bagaiman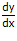a -nya?

Sama saja, begini caranya:

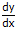= 2.5.x^(2-1)

 

= 10.x⁽¹⁾

 

Lalu kemana -10 nya?

Hilang karena turunan pertama konstanta adalah 0

 

Ada lagi?

Bila fungsi y = 5x²
– 10 diturunkan terhadap z (bukan x), dan ternyata x bukan fungsi dari z maka 5x² adalah merupakan konstanta sehingga turunan pertamanya terhadap z adalah:

= 0

 

Lalu bagaimana bila x merupakan fungsi dari z, misalkan x = z⁴?

Fungsi y = 5x²
– 10 diubah dengan mensubtitusikan fungsi z, sehingga didapat persamaan:

y = 5(z⁴)²
– 10

y = 5z⁶ – 10

 

sehingga:

 

= 6.5.z^(6-1)

= 30.z⁵

 

Cuma itu?

Sebagai dasar ya, akan tetapi masih ada lagi dan dapat dipelajari secara khusus dalam kalkulus, ini ringkasannya:

 

(1) y = C (C adalah lambang dari konstanta) => = 0

(2) y = C U(x) => 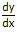= c . U`(x)

(3) y = U(x) ± V(x) => = U`(x) ± V`(x)

(4) y = U(x) . V(x) => = U`(x).V(x) + U(x).V`(x)

(5) y = => =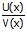

(6) y = f(U) dan U = g(x) => 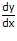= . (ini disebut bentuk rantai)

 

(7) y = ln(x) => =